Idea of PRiMAL
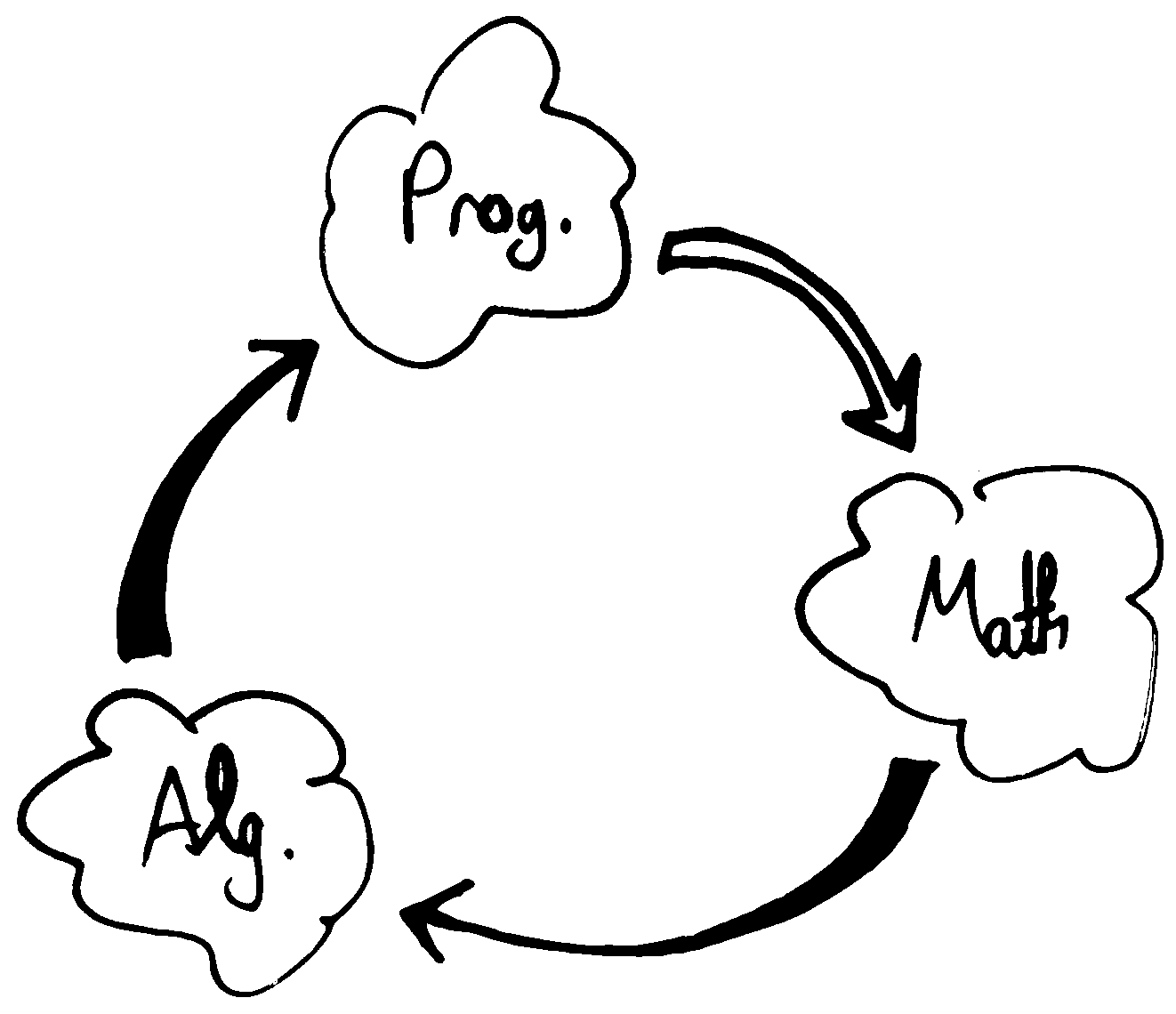
We propose a novel cyclic process (as depicted above) by which we start in one of three computational domains: programming, math, or algorithms; and cycles through them in that order, so as to make each pass enhance the next, until a certain discovery is made. The value of such an approach is two-fold. First, it integrates different elements of computational thinking that are essential for computer scientists and problem solvers in general. Second, it mimics to a great extent a natural process of learning, where people move from concrete observations (output of a PRogram), to conceptualization and hypotheses (Math), to active experimentation based on hypotheses and what has been learned (ALgorithms); new algorithms in turn can yield better programs and close the cycle.

In a computational field, the transition from Math, to Algorithms, to Programming may or may not be trivial, but it is definitely a natural one. It's the transition from Programming to Math (indicated by a white arrow in Figure 1) where the magic happens. This could be a moment when we put ourselves in an active learner mode rather than simply being receivers of information (thus enabling themselves to become independent thinkers). After observing the output of the programs, possibly by running them with different parameters each time, we can draw conclusions and conjecture a hypothesis. This will jump-start the mathematical exploration now that we know what to look for. It will also convey that programming is not just about writing code, and cultivate a skill for abstraction and generalization that is much needed in computational thinking and problem solving.

The following scenario will illustrate and motivate how, through computational thinking, the cyclic process of programming, math, and algorithms can guide us on a typical journey of discovery. Assume that we place a number $p\geq 3$ of points on a two-dimensional $n\times n$ grid, where $n>1$. Given $n$, how large must $p$ be to guarantee that three of the points make a right triangle? Observe that, with no guidance whatsoever, it is not clear how one would even approach this problem. But what if we write a program to experiment with small values of $p$ and $n$?

Level 1: Some will be comfortable to immediately start writing code and modifying it as they go. Others might think about an algorithm first to determine whether some right triangle exists. Regardless, the code/algorithm need not be efficient, so one could simply try all possible placement of $p$ points on an $n\times n$ grid and check every set of three points, which is feasible when $p$ and $n$ are small. By observing the output of the program for several small values of $p$ and $n$, we will be able to make a conjecture about $p$ as function of $n$. One will now embark on a mathematical adventure knowing precisely what statement to prove, and will be guided through this phase by exploring various proof techniques. Once the existence of right triangles is established, we might be asked to quickly find such a triangle when $n$ is large; for instance, if the points keep moving on the grid. We are back to algorithms. Any attempt must now be accompanied by algorithmic analysis to claim the efficiency. Guidance will also be provided here by considering different types of data structures.

Level 2: One could go even further to ask for the minimum number of right triangles we can guarantee. For instance, the algorithm can be modified to count all triangles for small values of $n$ and every placement of the points. By observing the output of the program again, one will conjecture a minimum and move to another mathematical exploration, thus cycling twice through the PRiMAL process.