Living on a random torus
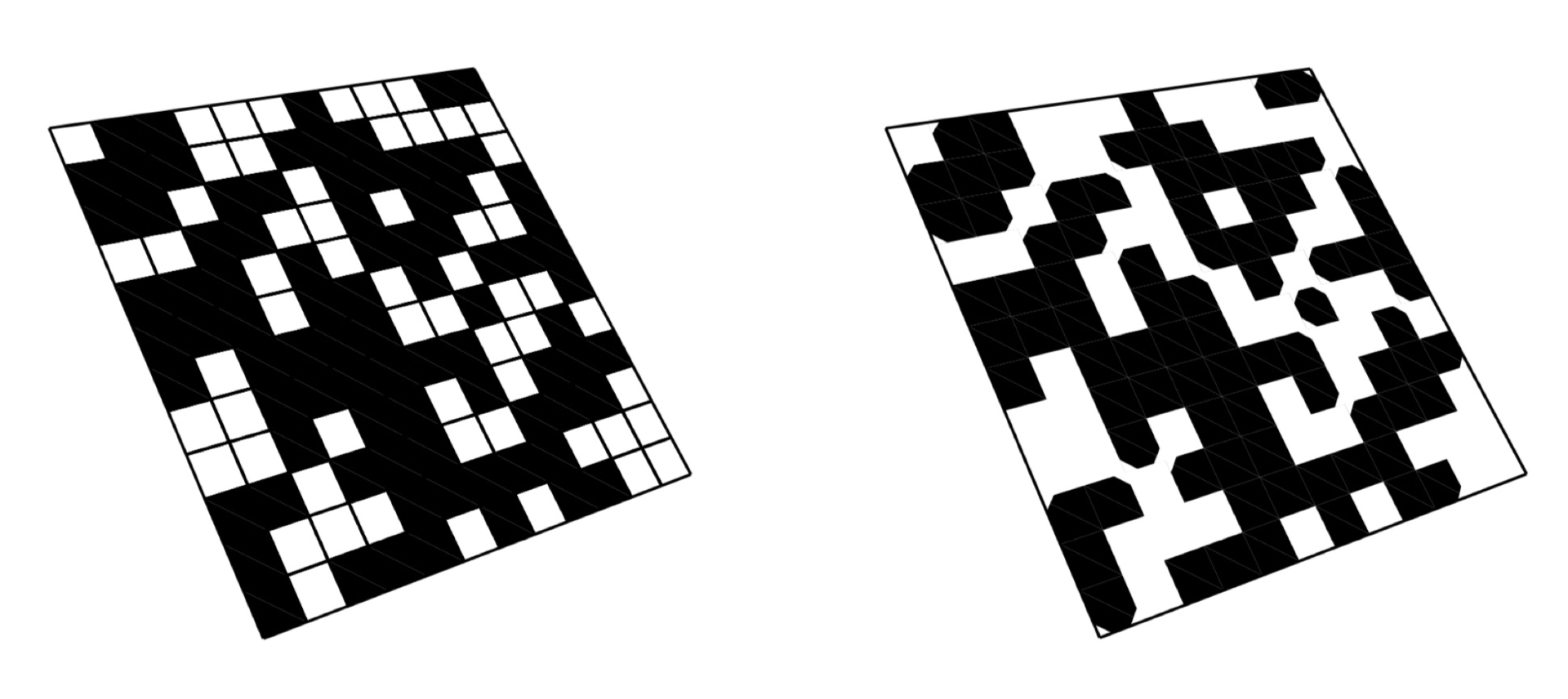
We don't see doughnut shapes in the sky, but can we imagine living on one? The closest concepts are the planet Saturn and the novel Ringworld (1970s). But for someone working with two-dimensional arrays, this could be a lot of fun. In an $n\times m$ array, each $a[i,j]$ is initialized to be 1 (land) with probability $p$ and 0 (water) with probability $q=1-p$. To avoid programming nightmares, we may assume that every $a[i,j]$ has four neighbors: $a[(i\pm 1) \bmod n, j]$ and $a[i, (j\pm1) \bmod m]$, thus a torus is born. Define an island as a maximal set of 1s that can be reached from one another by moving through neighbors and without crossing any 0s. Define a pool as a maximal set of 0s that can be reached from one another by moving through neighbors and diagonally, and without crossing any 1s. It is this asymmetry in the definition of islands and pools that will make the results interesting. In the following figure, we have 4 islands and 2 pools.

For what value of $p$ do we expect the same number of islands and pools? It is very natural here to start with a program that counts the number of islands and pools. But this would probably require a little bit of thought first: an algorithm. Some exposure to data structures and algorithms is helpful. For instance, a standard recursive DFS for connected components in a graph can be used. We can then generate statistical data about the absolute value of the difference between the number of islands and the number of pools for many values of $p$, and use desmos for instance to visualize the results.

The special value of $p$ for which this difference is minimized can now be investigated mathematically. This type of research requires probabilistic analysis and the use of expectations. But once $p$ is found, it can influence another algorithmic journey to address a more in depth look at the actual expected number of islands and pools. What is that number when both are equal? How does it grow with the size of the torus? Can visualizing this growth help discover some interesting constants; for instance, like in $cn^k$ for an $n\times n$ torus and some constants $c$ and $k$?

An advanced feature of this research could examine the hierarchical nature in which islands and pools alternate by containing each other, possibly forming a tree structure starting from the largest island. The problem can also consider other types of arrangements and notions of neighborhood for both islands and pools. For instance, what about triangular or hexagonal lattices?