Three points make a right triangle
Given $p\geq 3$ points on a two-dimensional $n\times n$ grid where $n>1$, how large must $p$ be to guarantee that three of the points make a right triangle? The following figure shows an example with $n=5$, $p=8$, and no right triangles.

Refer to the introductory section of PRiMAL for a detailed discussion on how this problem is exemplary for the PRiMAL cyclic process (-->PR-->M-->AL-->), with strong research components in programming, math, and algorithms.

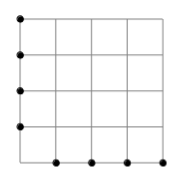
One could further add an interesting wolframalpha component to explore the use of matrices: The grid may be encoded as the adjacency matrix of a bipartite graph, where a point in row $i$ and column $j$ becomes the edge $(i,j)$. The number of right triangles that align with the x-axis and the y-axis can now be computed using matrix operations, because such triangles become analogous to paths of length 3 in the bipartite graph. This also draws our attention to the fact that some right triangles may not be aligned with the axes. The problem can be nicely generalized to $n\times m$ grids, higher dimensions (e.g. 3D), and other shapes; for instance, one could be looking for rectangles instead of right triangles.