
Polymath Jr. REU
Explore with sequences, patterns, and programming...
My project in Polymath Jr. 2024 will focus on ideas in infinite Skolem sequences. Four students will present their work on this project at the PME session of JMM 2025 in January. Some pictures at the conference can be found here. An elaborate list of results can be found towards the end of this page.
Infinite Skolem sequences
A Skolem sequence for $n\in\mathbb{N}=\{1,2,3,\ldots\}$ is a sequence of $2n$ integers such that every integer $i\in\{1,2,\ldots,n\}$ appears in exactly two positions at a distance $i$. An example for $n=4$ is $1,\ 1,\ 3,\ 4,\ 2,\ 3,\ 2,\ 4$ (the distance between the two copies of an integer is equal to that integer). Skolem sequences exist for $n\equiv 0,1 \pmod{4}$, but they are not trivial to construct. On the other hand, an infinite Skolem sequence, defined as $\{s_i: i\in\mathbb{N}\}$ where every $n\in\mathbb{N}$ appears in exactly two positions at distance $n$, can be obtained easily: Having placed two copies of $1, 2, \ldots, n$, one idea is to place the first copy of $n+1$ in the first available position, and the second at the appropriate distance. This gives the first lexicographic infinite Skolem sequence, where $n$ first appears before $m$ whenever $n\lt m$:
$$1,\ 1,\ 2,\ 3,\ 2,\ 4,\ 3,\ 5,\ 6,\ 4,\ 7,\ 8,\ 5,\ 9,\ 6,\ \ldots$$
A visual progression for this construction can be found below, and here's some illustration using Desmos:
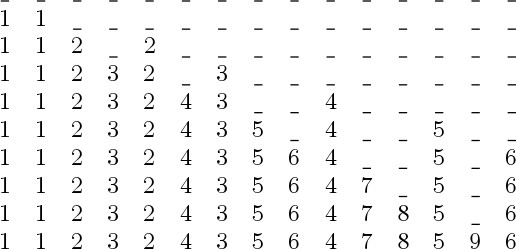
For any given $n$, let $a_n$ be the position of the first occurrence of $n$ in the infinite Skolem sequence above. How can we find $a_n$? One could start with a program to generate $s_1, s_2, \ldots, s_k$ in an array for a large enough $k$ and observe when $n$ first shows up. Since we don't know how large $k$ must be, an initial challenge is to work without this knowledge, or using structures that can be extended at run time. Obviously, there is a need for a better algorithm. By observing $a_n$ for different values of $n$, one may be able to conjecture lower and upper bounds on $a_n$. The program (or other types of explorations) can guide us to observe how the sequence $a_1, a_2, a_3, \ldots$ evolves, perhaps by looking at $a_{n}-a_{n-1}$ (see exercise 6 below suggesting a binary pattern). Once patterns emerge, OIES may be used to investigate whether anything is known about such patterns. Eventually, one could develop a better algorithm to compute $a_n$, possibly one that avoids arrays altogether.
The problem can be extended by requiring for each integer $n$ three copies at distance $n$. For instance, if we follow the above strategy, the infinite sequence will begin with: $$1,\ 1,\ 1,\ 2,\ \underline{3?},\ 2,\ \underline{\ \ \ },\ 2,\ \underline{\ \ \ },\ \underline{\ \ \ },\ \underline{\ \ \ },\ \ldots$$ However, by attempting to place 3 starting at the first available position, its second copy will be blocked by the last occurrence of 2! Following this strategy, 4 will have to be placed before 3. But this repeats, and the first occurrence of 3 will have to wait until position 28. Therefore, the first lexicographic infinite Skolem sequence in this case does not have a monotonic $a_n$. In general, if we have $k>2$ copies of each integer, which integers will be blocked, and will they ever find their place in the sequence? What is an algorithm for constructing such an infinite sequence, and how is $a_n$ affected? What if we relax the rules to have $k$ copies of each integer, but require that only two consecutive copies must be at distance $n$? Each choice of the two copies changes the pattern for $a_n$ and defines a separate problem. Here's an example when $k=3$ and the last two copies must be at the correct distance (observe that $a_n-a_{n-1}-2$ is also binary, it is either 0 or 1). $$1,\ 1,\ 1,\ 2,\ 2,\ 3,\ 2,\ 3,\ 4,\ 4,\ 3,\ 5,\ 5,\ 4,\ 6,\ 6,\ 7,\ 5,\ 7,\ 8,\ 8,\ 6,\ 9,\ldots$$
Prerequisites
Experience in discrete math, proofs, algorithms, and programming (not necessarily all).
Mentoring team
The team consists of:
- Professor Saad Mneimneh (myself), Hunter College of the City University of New York,
- his Guinea pig Chanel,
- Saman Farhat, a former PhD student who worked on the problem,
- Benjamin Garrett PhD, Adjunt Assistant Professor at Hunter College,
- Paul Cesaretti, Graduate Center of CUNY, and
- Ryan Vaz, an undergraduate student from Hunter College.
Participating students
A list of participants with picture, email, and info can be found here.
Recordings (lectures introducing the subject during the first week)
- Introduction, passcode: a0SYK=#7
- Existence of Skolem sequences, STS (Steiner Triple System), passcode: &^THe8T=
- STS(6n+1) connection to Skolem sequence, Wythoff pairs and the game of Nim, passcode: +V0b=Scr
- Infinite Skolem sequences and the spectrum of irrational numbers, passcode: #vwWG!62
Note: $f(n)=\lfloor nq\rfloor - \lfloor np\rfloor$ is not necessarily surjective nor injective on $\mathbb{N}$. For instanace, when $p=\sqrt{2}$ and $q=2+\sqrt{2}$, only even distances are represented. In addition, when $p=\sqrt{3}$ and $q=(3+\sqrt{3})/2$, multiple values of $n$ produce the same distance. - More on infinite Skolem sequences, passcode: #?ZDAM2L
- Skolem sets, passcode: W%7u!t1Q
How to proceed (after lectures)
Here's how to proceed and a Google form to fill.
Weekly meetings (zoom only)
Next meeting (passcode: 1123243564) is Wed. Aug. 7, 2024 at 12:00 PM.
- Here's a summary of the July 3, 2024 meeting.
- Here's a recording of the July 10, 2024 meeting (passcode: zq.7^mJp).
- Here's a recroding of the July 17, 2024 meeting (passcode: E8XSW_i_).
- Here's a recording of the July 24, 2024 meeting (passcode: KQ$QYz4o).
- Here's a recording of the July 31, 2024 meeting (passcode: eE9QCes*).
Office hours (zoom only)
- Saad's office hours, passcode: Oh7223. Mondays 12:00 PM - 2:00 PM
- Paul's office hours, passcode: 1234. Tuesdays 10:00 AM - 12:00 PM.
- Saman's office hours, passcode: 5TmJn7. Tuesdays, Thursdays 3:30 PM - 4:30 PM.
- Benjamin's office hours. Fridays 3:00 PM - 5:00 PM.
- Ryan's office hours, passcode: 780208. Tuesdays, Thursdays 5:00 PM - 6:00 PM.
Overleaf document (this is where we keep our progress)
Make sure to create an Overleaf account. To access the document,
click here. Create a file with your name to report progress, questions, code, etc...
Slack workspace
You can join here.
Some preliminary ideas on this problem
- My paper in computer science education (the first problem is about the infinite Skolem sequence).
- A manuscript I wrote with Saman Farhat showing a connection to the rabbit sequence (the complement of the infinite Fibonacci word).
- Part of a presentation I gave at MoMATH in May 2024.
- Does an infinite Skolem sequence optimize anything? (Yes.)
More references related to Skolem sequences (most can be found by a simple search, just cut and paste into Google...)
- Th. Skolem. On certain distributions of integers in pairs with given differences. Mathematica Scandinavica, pages 57–68, 1957.
- Th. Skolem. Some remarks on the triple systems of Steiner. Mathematica Scandinavica 6, pages 273-280, 1958.
- Langford sequences (related), here.
- Perfect Skolem sets, G. Nordh, Discrete Mathematics 308(9), May 2008.
- Harold Scott Macdonald Coxeter. The golden section, phyllotaxis, and Wythoff ’s game. Scripta Mathematica, 1953.
- Willem A. Wythoff. A modification of the game of nim. Nieuw Arch. Wisk, 7(2):199–202, 1907, also here.
- Nabil Shalaby. Skolem sequences: generalizations and applications. PhD thesis, McMaster University, 1991.
- S. Eldin, N. Shalaby, F. Al-Thukair. Construction of Skolem sequences. International Journal of Computer Mathematics, 1998, here.
- C Reid. Extended near-Skolem type sequences, infinite Skolem sequences, and related topics. PhD thesis, Memorial University of Newfoundland.
- Nevena Francetic and Eric Mendelsohn. A survey of Skolem-type sequences and Rosa's use of them. Math Slovaca 59, 2009.
- V. Linek. Extending Skolem sequences, how can you begin? Australiasian Journal of Combinatorics 27, pp. 129-137, 2003.
- Thomas R. Bewley. Pairwise-nonrecurrent sequences.
- David Churchill. Algorithms for constructing generalized Skolem-type sequences. Thesis, 2005.
- A. Assarpour, A. Bar-Noy, O. Liu. Counting Skolem sequences. arXiv 2017.
- Ron Knott. The golden string of 0s and 1s, online.
Warm up exercises (and some useful programming tasks)
Some warm up exercices are added to the Overleaf document (link above in the Overleaf section). As an initial learning component, you will be guided to work on specific exercises based on your interests and the research direction you are involved in. Solutions and answers will eventually be added. Students can also contribute to programming/math solutions if they like... Some of the exercises are reproduced here for those who are interested.
- Find (finite) Skolem sequences for $n=1$, $n=4$, $n=5$, and $n=8$.
- Consider the following pattern: $f_0=0$, $f_1=01$, and $f_n=f_{n-1}f_{n-2}$ (concatenation). The infinite Fibonacci word is given by the limit of this pattern when $n$ goes to infinity. Generate the first few bits of the infinite Fibanacci word, and use OEIS to verify that your initial few bits are correct.
- Start with 01. Scan the pattern starting at the second bit (the 1). If you encounter a 0, append a 01 to the end of the pattern, and if you encounter a 1, append a 0 to the end of the pattern. Verify that this is also equivalent to the definition of the infinite Fibonacci word.
- Write a program to generate the first $n$ bits of the infinite Fibonacci word.
- Write a program to generate the first $n$ numbers in the infinite Skolem sequence $1, 1, 2, 3, 2, 4, 3, 5, 6, 4, 7, 8, 5, 9, 6, \ldots$.
- Consider the infinite Skolem sequene where every integer $n$ appears $k=3$ times, and every consecutive copies of that integer are at distance $n$. Verify that $a_3=28$ if we favor the sequence that comes first in a lexicographic order.
- Prove that $\lfloor n\phi^2\rfloor-\lfloor n\phi\rfloor=n$ for $n\in\mathbb{N}$, where $\phi=(1+\sqrt{5})/2$. What is the significance of this in the context of infinite Skolem sequences? Can you revisit exercise 5? Here's an illustration using Desmos.
- Would you like to come up with a Skolem-like infinite sequence, or a particular construction of one, using alternative rules? Go for it and share your ideas... For instance, my student Vlad Vostrikov suggested the following variation to the construction of the Skolem sequence with three copies, where 3 is shown to be blocked in the above example: place $n$ in the first available position that does not lead to a block. This makes the sequence not the first in a lexicographic order, leading to $1,\ 1,\ 1,\ 2,\ ? ,\ 2,\ 3,\ 2,\ 7, 3,\, 4,\ 5,\ 3,\ \ldots$ as opposed to $1,\ 1,\ 1,\ 2,\ 4,\ 2,\ 5,\ 2,\ 4,\ 6,\ 7,\ 5,\ 4,\ \ldots$. Initially the question was: will every integer be placed? With the variation the question becomes: will every position be filled?
Some research questions (we will write code to discover patterns and/or explore strategies when the math is too obscure)
- [All exact distances] Consider the infinite Skolem sequence where each integer $n$ appears exactly three times in positions $a_n$, $b_n$ and $c_n$, such that $b_n-a_n=c_n-b_n=n$. Can such sequence be constructed, and how? There are two basic ideas for the construction: 1) Place $n$ in the first available position only if the other two copies can also be placed. 2) Place $n$ in the first available position that allows the placement of the other two copies. Each approach has its challenges in proving that the construction works. In addition, what is $a_n$? If, instead, we drop integers that don't immediately fit in the first available position, what do we end up with? Can the work be generalized to more than 3 copies?
- [One exact distance] Consider the infinite Skolem sequence where each integer $n$ appears $k\geq 3$ times, but only the $i^{\textrm{th}}$ and the $(i+1)^{\textrm{st}}$ copies must be at distance $n$. A special case is when $i=1$. Another case is when $i=k-1$. For both of these cases, $a_n$ can be found. In particular, for the case of $i=k-1$, $a_n$ can be expressed in terms of a sum of bits of some infinite binary sequence that we know (observed and formulated by Saman Farhat, see this presentation for instance). We don't have a proof of this fact yet for a general $k$. Other cases for $i=2,\ldots,k-2$ can be studied as well. If $a_{n,i}$ is the position of the $i^{\textrm{th}}$ copy of $n$, is $a_{n,i}$ given by $\lfloor np\rfloor$, where $p$ is some irrational number? How can we get $a_{n,1}$? Another idea for an infinite Skolem sequence is to have $2k$ copies for every integer $n$, such that the copies can be grouped in pairs, and each pair is at distance $n$. What kind of properties do we get for this variation? For instance, when $k=2$, we have $1,\ 1,\ 1,\ 1,\ 2,\ 2,\ 2,\ 2,\ 3,\ 3,\ 4,\ 3,\ 3,\ 4,\ 4,\ -,\ -,\ 4,\ \ldots$
- [Optimization and offline/online algorithms] (this idea/approach is due to Saman Farhat) Consider a given set of integers. How can you palce two copies of each at the appropriate distance in such a way to minimize gaps? For instance, it is always possible to have at most $m-1$ gaps by placing the smaller numbers first in the first available position, where $m$ is the largest integer. Here's an example: If $S=\{1,10\}$, then we can place $1,\ 1,\ 10,\ -,\ -,\ -,\ -,\ -,\ -,\ -,\ -,\ -,\ 10$. But we can do better. In general, what is the best strategy? What if our algorithm is online? In other words, we can only see one integer at a time, but we must place that integer before seeing the next. What about a randomized strategy (online and offline)? Another idea contributed by Paul Cesaretti includes adding a buffer for the online algorithm. How does that affect the optimization of the number of gaps?
Some results of this REU
-
The following will be presented at the PME session of JMM 2025:
- Ben Gildea, Saman Farhat, Saad Mneimneh, An Investigation into n-Copy Skolem Sequences, JMM 2025.
- Ahan Chaterjee, Saad Mneimneh, Approximate Infinite Skolem Sequences, JMM 2025.
- Sambhu Ganesan, Jack Rosenthal, Saman Farhat, Saad Mneimneh, Relaxed Infinite Skolem Sequences, JMM 2025. The following is a more elaborate list of results obtained:
- Proof of existence of infinite $k$-Skolem sequences. (Ben)
- The set of infinite $k$-Skolem sequences is uncountable. (Ben)
- Study of some ordering of $k$-Skolem sequences. (Ben)
- Given that integers fall in $\{1,2,\ldots, n\}$, there exists an online algorithm that achieves $O(\sqrt{t})$ gaps (where $t$ is time). (Jack)
- Given that integers fall in $\{1,2,\ldots, n\}$, there exists an online strategy with $O(n^2)$ buffer an no gaps (possibly, buffer size can be reduced to $O(n)$). (Jack)
- The offline strategy of placing the smaller integer first achieves $O(n/\phi)$ gaps asymptotically, assuming the integers received are $1, 2, \ldots, n$. (Jack)
- The offline strategy of placing the largest integer first achieves $\approx 0.08n$ gaps, assuming the integers received are $1,2,\ldots,n$. (empirical). (Jack)
- The relaxed Skolem sequence with $k$ copies where the first two are required to be at the correct distance satisfies $a_n=n+(k-1)(2^{\lfloor\log_2n\rfloor}-1)$. (Jack)
- The relaxed Skolem sequence with $k$ copies where the last two are required to be at the correct distance satisfies $a_{k-1}=\lfloor n\phi_k\rfloor$, where $\phi_k=(k-1)(1+\sqrt{1+4/(k-1)})/2$, and $a_i$ is the position of the ith copy. In addition, for $i\lt k-1$, $a_i=\lfloor[(k-1)n-(k-1-i)]\phi_k/(k-1)\rfloor$. (Sambhu)
- The exists a $k$-copy Skolem sequence (with an explicit construction), where the distance between every two consecutive $n$'s is $b^n$, where $b$ is any positive integer. (Sambhu)
- One can construct an approximate $k$-Skolem sequence where the distance between any two consecutive copies of $n$ devidates from $n$ by at most a constant related to $k$. This is part of a study of $k$-Skolem sequences, beaty sequences, and spectrums of irrational numbers. (Aahan)
- There exists two infinite 3-copy Skolem sequences, each covering a subset of the integers, such that the two subsets partition $\mathbb{N}$ (so far, empirical). (Luca)
- There exists a 2-copy Skolem sequence in two dimentions such that the two copies of $n$ are at manhattan distance equal to $n$. The same is true for a 3-copy Skolem sequence, where the manhattan distances are $n$, $n$ and $2n$. The same is true for a 4-copy Skolem sequence, where the mantattan distances are given by a square of $n$'s.
- The lexicographic construction of a $k$-copy Skolem sequence exists (empirical) (proof is in the works). (Valentio)
- The $k$-copy Skolem sequence obtained by placing the next number in the first gap that works seems to leave position 5 unfilled (empirical). (Valentio)
- The construction of a $k$-copy Skolem sequence that drops an integer from the sequence if it cannot fit in the first available gap satisfies $1/x+1/(1+x)+\ldots+1/(k-1+x)=1/(1-r)$, where $1/x$ ($x=\lim_{n\rightarrow\infty} a_n/n$) is the rate at which the first copy occurs and $r$ is the rate of dropping (empirical with almost a proof). (Valentio)
- A finite 3-copy Skolem sequence for $n$ must satisfy a necessary condition $n\equiv 0,1,\ldots,k-1 \bmod k^2$. If $k$ is not prime, one can further improve the necessary condition (Valentio).